NPV and IRR

Question

Anyone have a better explanation to figure this out? I got lost.. I tried putting in fake numbers and actually thought the answer was  A. Thanks in advance!
A company prepares a chart with the net present value (NPV) profiles for two mutually exclusive projects with equal lives of five years. Project Jones and Project Smith have the same initial cash outflow and total undiscounted cash inflows, but 75% of the cash inflows for Project Jones occur in years 1 and 2, while 75% of the cash inflows for Project Smith occur in years 4 and 5. Which of the following statements is most accurate regarding these projects?

Project Smith has a higher internal rate of return than Project Jones.
 	There is a range of discount rates in which the optimal decision is to reject both projects.
 	There is a range of discount rates in which the company should choose Project Jones and a range in which it should choose Project Smith.

Explanation

If the total undiscounted cash flows from two projects are equal, their NPV profiles intersect the vertical axis at the same value. The NPV profile will have a steeper slope for Project Smith, which has more of its cash inflows occurring later in its life, and therefore the IRR of Project Smith (its intersection with the horizontal axis) must be less than the IRR of Project Jones. The NPV for Project Jones will be greater at any rate of discount, and Project Jones will be preferred over the entire range. However, if the discount rate applied to the cash flows is greater than the IRR of Project Jones, both projects will have negative NPVs and the company should reject both of them.

cveto · Answer

This is a theoretical question, where the principles are important, not actually the numbers themselves.

Important facts:

initial cash outflows are the same for the 2 projects
 	both projects have equal lives of 5 years
 	both projects have the same cash flows over the 5 year period

Keeping these things in mind, lets go over the options:

a) The project with the cash flows occuring in the earlier periods will be subject to less fluctuation when discounting because the effect of "time value of money" will be for 1-2 years rather than for 20 year for example. This is true regardless of the interest rate chosen (5%, 25%, IRR,  required rate of return). Keep in mind that IRR is interest rate where NPV = 0.  With all things being equal as per the important things 1. 2. and 3. stated above, then the project with the higher IRR rate will be the earlier project (Project Jones), not Project Smith. This is because to compensate for the lower effect of time value of money, you will need higher interest rate to achieve IRR (where NPV = 0). Lets say, with 30% discount rate, you can achieve NPV = 0 for the Project Jones, but you will only need 25% discount rate needed to achieve IRR (NPV = 0) for Project Smith. The numbers are made up, they dont matter as long as you get the principle. Therefore, this option is FALSE.

b) This is a general statement. The thing about general statements is that they have to hold true regardless of the circumstances (that is why they are general statements and not specific statements). With that in mind, the easiest thing to "TEST" the validity of a general statement is to go the "EXTREME". Lets say, what if the Interest rate is 1000000000%? Of course with such high interest rate, the discounting of cash flows regardless of whether they are in years 1-2 (Project Jones) or 4-5 (Project Smith), the effect will still be ENORMOUS. The decision criteria for NPV is choose projects with POSITIVE NPVs. Now the cash flows will be minimised by the discounting, but what about the initial investment (i.e. cash outflow)? It occurs today (no discounting effect). Therefore, even at RIDICULOUS discount rate, such as 1000000000%, it will still be the same amount. Therefore, there is a range of interest rates where the project should be rejected (even if that range is ridiculous). This goes for both Project Jones and Project Smith. Therefore, this option is CORRECT.

Please see example below, where the initial investment today (time 0) is 100 dollars and it will bring you a cash flow of 10 million in 1 years time. Sounds good, right? At discount rate of 99999999%, however, the project will still be loss making (negative NPV) and will be rejected. This is to illustrate that there is, in fact, a range of interest rates where the project will be at a loss.

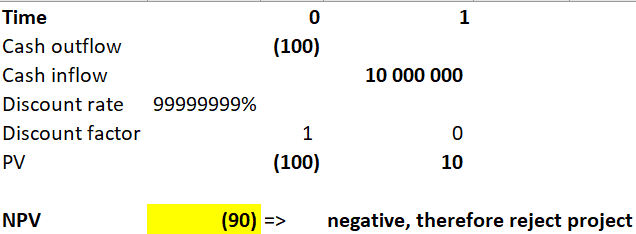
c) Again, general statement. Because of the "important facts" mentioned above, Project Jones will always be more beneficial than Project Smith because of time value of money (receiving the same inflows of cash flows earlier rather than later). This holds true for all, interest rates.

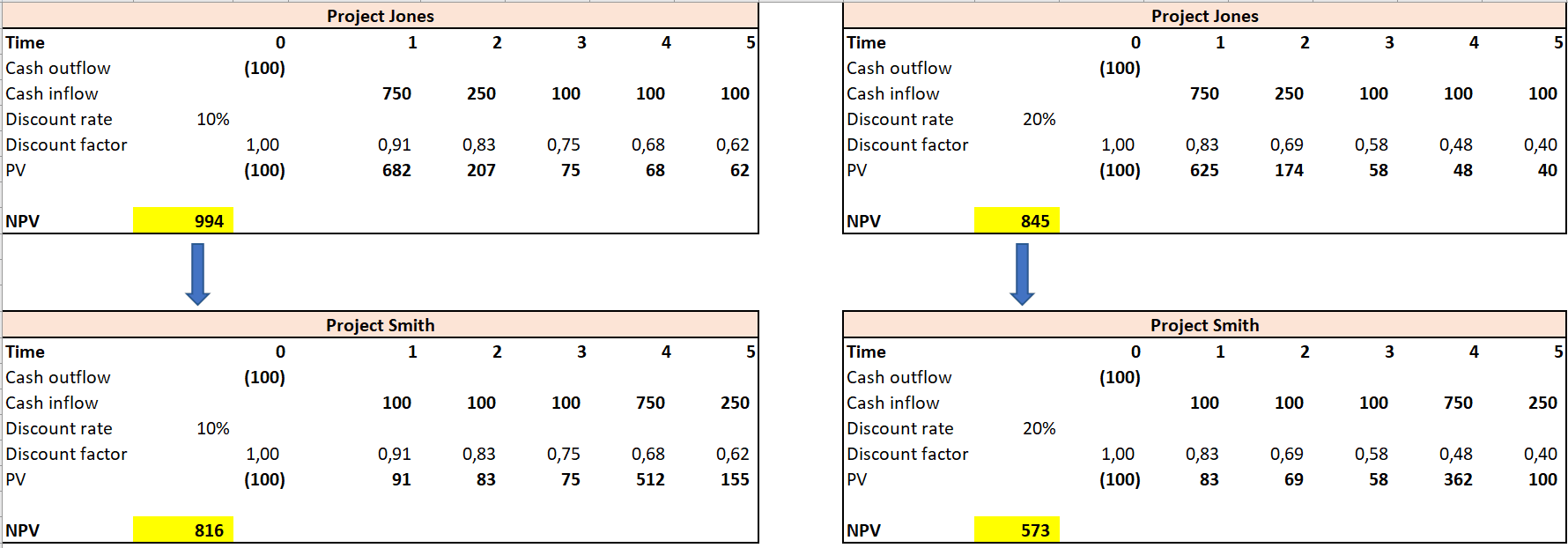
Please see attached an illustration which fulfils the criteria:

same initial cash outflow of 100 for both projects
 	same life of 5 years
 	same total cash inflows over the 5 years (1300 total inflows)

With interest rate of 10%, project Jones will have NPV of 994 whereas Project Smith only 816. With 2 mutually exclusive projects (i.e. you can only invest in 1), you will invest in the one with the higher return (NPV) => therefore Project Jones. With interest of 20%, NPV of Jones is 845 whereas NPV of Smith is only 573 (again Jones win). This holds true for ALL possible interest rates! Note that the proportion of the cash flows in year 1-2 may not be 75% as mentioned in the QUESTION, but it doesnt matter, the principle still holds true. This is only true because of the restrictions (same cash outflow, same cash inflow, same lives, only different timings). Therefore, Project Smith will NEVER be better all these things being equal and this statement is FALSE.

cveto · Answer

it is difficult to explain concepts and generalisations using words and makes for a very lengthy answer @zee hope the numerical examples help the person asking, picture does paint a thousand words :)